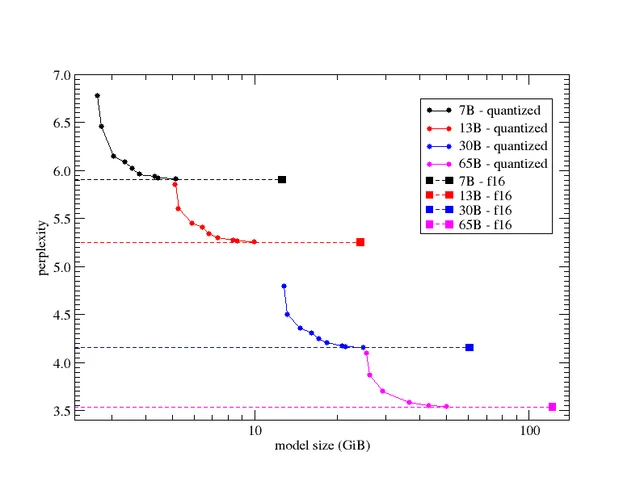
困惑度(Perplexity)是评估语言模型(LLM)性能的关键指标。它衡量模型在预测文本序列时的不确定性程度,用于量化模型对未见过的数据的预测能力。
困惑度的定义与计算
- 数学定义: 困惑度是模型对测试集的对数概率的负平均值。数学上表示为: $$\text{Perplexity} = \exp\left(-\frac{1}{N}\sum_^{N}\log p(x_i)\right)$$ 其中 N 是测试集中的标记数量,p(x_i) 是模型对标记 x_i 的预测概率。
- 直观理解: 困惑度可以理解为模型在每个位置上平均需要考虑的可能选项数量。困惑度越低,说明模型的预测准确性越高。
- 熵的关系: 困惑度是序列交叉熵的指数,直接反映了模型预测的不确定性。
困惑度的重要意义
- 模型评估: 困惑度提供了一种客观的方式来比较不同语言模型的性能,是训练过程中的重要监控指标。通常微调或者量化过程中也会使用。
- 过拟合检测: 通过比较训练集和验证集上的困惑度,可以发现模型是否过拟合。
- 预测质量: 较低的困惑度通常意味着模型能够生成更流畅、更连贯的文本。
- 领域适应性: 困惑度可以反映模型在特定领域文本上的表现,帮助评估模型的领域迁移能力。
困惑度的使用场景
困惑度广泛应用于各种 LLM 相关的场景:
- 模型训练: 作为训练过程中的优化目标和停止条件。
- 模型选择: 帮助研究人员在不同架构和参数设置之间做出选择。
- 数据质量评估: 高质量的训练数据通常会导致模型在相似数据上具有较低的困惑度。
- 生成文本评估: 虽然不是唯一指标,但困惑度可以作为生成文本质量的参考。
困惑度的局限性
尽管困惑度广泛使用,但它也存在一些局限性:
- 不完全反映语义理解: 低困惑度不一定意味着模型真正理解了文本的语义。
- 对于开放式生成任务不够全面: 在创意写作等任务中,困惑度可能无法完全捕捉输出的质量。
- 与人类评价不完全一致: 困惑度是一个统计指标,可能与人类对文本质量的主观评价存在差异。
- 模型大小的影响: 大型模型往往能够达到较低的困惑度,但这并不总是转化为更好的实际应用效果。
总之,困惑度是评估 LLM 性能的重要指标,提供了一种客观测量模型预测能力的方法。然而,它应该与其他评估方法结合使用,以全面了解模型的实际性能。